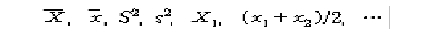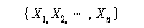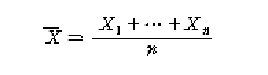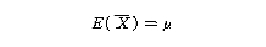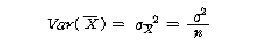[스크랩] 통계기초10:통계량

-- 3-2 통계량

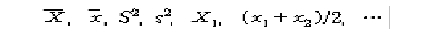
-- 흔히들 어떤 수치를 통계라고 한다.     이를테면, 전세계의 연도별 기아 사망자수 통계, 통화량, 통계, 자동차 통계 등등 통계라고      표현하는 것의 정확한 용어는 통계량(statistic)이다. -- 통계량이란 표본으로부터 얻어진 어떤 것으로 정의된다. 즉, (X1,X2,X3........Xn)또는     (x1,x2,x3.......xn)으로부터 얻어진 결과를 통계량이라고 한다. --     예를 들면 등 통계량의 형태는 무수히 많다.             여기서 중요한 것은 확률변수 형태의 표본, (X1,X2,X3........Xn)으로부터 얻어진 통계량은     하나의 또 다른 확률변수로서 어떤 분포를 한다는 것이다. 즉, 앞의 예 중에서  X, s, s2 은     어떤 분포를 한다는 점이다. -- 이제, 모집단과 표본의 관계로 부터 통계량을 이해해 보자.     모집단의 크기가 N이라고 한다면 표본의 크기 n은 훨씬 작은 값일 것이다.     표본은 모집단으로부터 얻어진 것은 물론이다. 그러면, 통계량은 어떤 목적으로 얻는 것일까?     모집단에 대해 알고자 하는 어떤 값을 파라메터(parameter)라고 하는데 파라메터 값을     직접적으로 알 수는 없으므로 표본으로부터 얻어진 값, 통계량으로써 파라메터를 알아내자는     것이다.     이와 같은 과정을 추정이라고 하는데 뒤에서 다루게 될 것이다. -- 파라메터 중에서도 가장 중요한 것은 역시 평균이다. 즉, 모집단의 무수히 많은 값들을 -- 대표하는 하나의 값이 평균이기 때문에 평균으로써 그 모집단의 특성을 한마디로 표현하고자 -- 하는 경우가 많다. -- 수많은 대학생들의 등록금 인상액 평균, 서울시 세대별 전력사용량 평균, 어느 건설회사의 -- 월평균 사고건수 등등 평균이라는 파라메터로써 우리가 알고자 하는 바를 나타낼 수 있는 -- 경우가 허다하다. -- 그러면, 모집단의 평균을 알아보고자 할 경우, 우리는 어떻게 할 것인가?     모집단으로부터 표본을 얻고 표본의 평균을 구함으로써 모집단의 평균에 관한 궁금증을 해결할     수 있을 것이다. 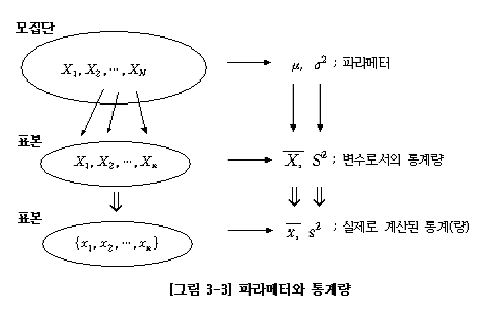-- [그림 3-3]은 모집단과 파라메터, 이에 대응되는 표본과 통계량의 관계를 나타내고 있다. -- 모집단의 크기가 N일 경우, 모집단으로부터 표본크기 n의 표본을 얻어서 모집단에 대해 -- 알고 싶은 파라메터 값들을 통계량으로써 추정하게 된다는 과정을 보여주고 있다.

3-3 표본평균의 분포

-- 모집단으로 얻게되는 표본의 평균은 표본이 어떻게 얻어졌느냐에 따라 그 표본평균값이 다르게 -- 된다.     이를테면, 모집단이 1000개의 개체로 구성되어 있을 경우, 1000개중에서 어떤 개체가 선택 -- 되느냐에 따라 표본의 구성이 달라지므로 1000개에서 100개를 고르는 경우의 수 1000C100 개나     되는 서로 다른 표본이 가능하다. -- 그 표본평균 값들 중에는 같은 값도 있겠고 서로 다른 값들도 있을 것이다.     이렇게 표본평균값들이 여러 개 존재할 수 있으므로 표본평균값들의 분포가 있게 되고     이를 표본평균의 분포라 하는 것이다. -- 예를 들어, {0, 1, 2, …, 14}의 값들을 갖고 있는 15개의 카드로 모집단이 구성되어 있다고 하자. -- 이 모집단으로부터 표본크기 n=6의 표본을 얻고자 할 때, 얻어질 수 있는 가능한 표본들의 수는 -- 15C6, 즉, 5005개의 서로 다른 표본들이 있게 된다. 이를테면,

-- 등의 서로 다른 표본들이 존재하므로 각 표본들에 대한 표본평균값들이 5005개 얻어질 수 있다. -- 이들 5005개의 표본평균값들은 가장 작은 값 (2.5, {0, 1, 2, 3, 4, 5})에서 가장 큰 값 -- (11.5, {9, 10, 11, 12, 13, 14}) 사이에 분포되어 있을 것이고 그 중에서는 같은 값들도 있을 -- 것이다.     이들 5,005개의 표본평균값들의 분포를 표본평균의 표본분포라고 하는데 복잡한 용어이므로     간단히 표본평균의 분포라고 부르기로 하자.     물론, 우리들은 실제에 있어 단 하나의 표본, 을얻는 것이며 -- 그의 표본평균값 를 얻게 되는 것이다. -- 이와 같은 사실을 이론적으로 설명해 보면 다음과 같다. -- 이론적인 표본    은 n개의 확률변수로 구성되어 있다.    각각의 X는 모집단의 분포, 즉, f(X)의 확률분포를 한다고 하였다.       그러면, 표본의 평균 X바는

-- 이므로 X바 또한 확률변수이고 확률분포를 한다는 것이다. X바가 어떤 분포의 형태를 갖는가는 -- 잠시 후에 알아보기로 하고, 먼저 확률변수 X바의 평균과 분산을 구해보면 다음과 같다. 즉,

---- (3-2)

---- (3-3)

-- 이다. -- 이론적으로 생각해 볼 때, 모든 가능한 표본평균값들의 평균은 전체의 평균, 즉 모집단의 평균이 -- 될 것은 당연한 결과이다.     또, 표본평균들의 분산은 모집단의 분산을 표본의 크기 n으로 나눈 -- 것으로 얻어진다.

         

          모 수                 명칭                통계량

               m                    평균                    X바

            σ2                   분산                    s2

            σ                 표준편차                 s

출처 : deep look

글쓴이 : 딥룩 원글보기

메모 :